代码的鲁棒性

# 代码的鲁棒性

[TOC]

鲁棒是Robust的音译，也就是健壮和强壮的意思。 鲁棒性（robustness）就是系统的健壮性。它是指一个程序中对可能导致程序崩溃的各种情况都充分考虑到，并且作相应的处理，在程序遇到异常情况时还能正常工作，而不至于死机。

# 一、链表中倒数第k个结点

# 1.1题目描述

输入一个链表，输出该链表中倒数第k个结点。

# 1.2解法

# 1.2.1双指针法

一个指针置于head,另一个指针在k-1位置，然后一起走呀走……

/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/
function FindKthToTail(head, k)
{
    if(!head||k<=0) return false;
    let p1=head,p2=head;
    for(let i=1;i<k;i++){
        if(p2.next){p2=p2.next;}
        else{return false;}
    }
    
    while(p2.next){
        p1=p1.next;
        p2=p2.next;
    }
    return p1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 1.2.2转数组无脑法

20ms 13156k
function FindKthToTail(head, k)
{
    let arr=[];
    while(head){
        arr.push(head);
        head = head.next;
    }
    return arr[arr.length-k];
}

1
2
3
4
5
6
7
8
9
10

# 二、反转链表

# 2.1题目描述

输入一个链表，反转链表后，输出新链表的表头。

# 2.2解法

# 2.2.1非递归解法

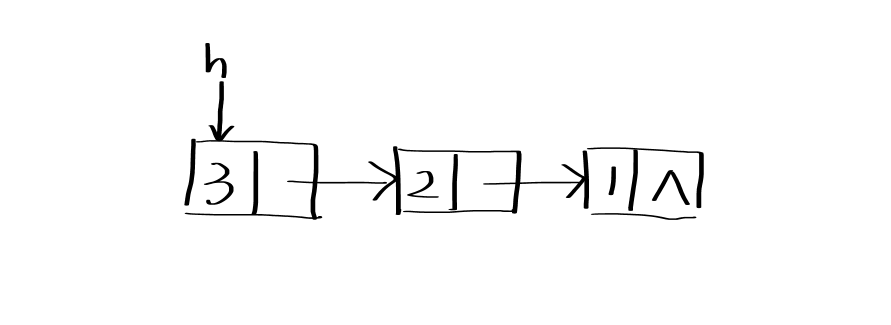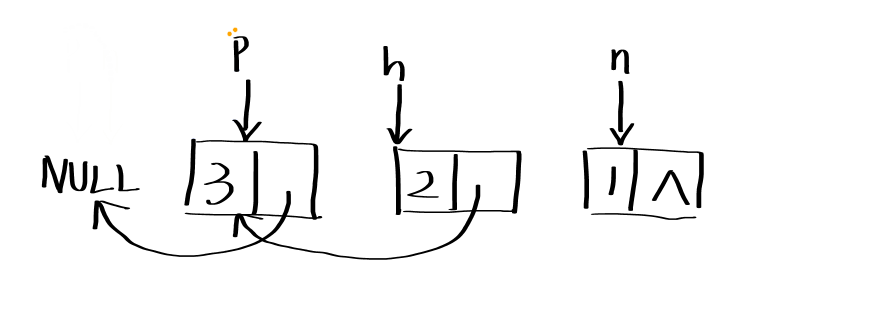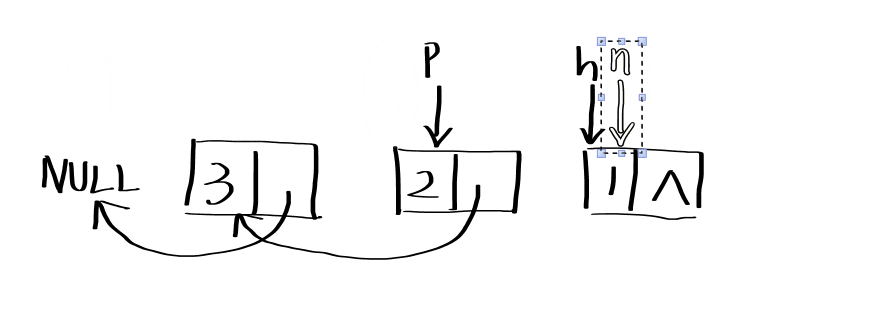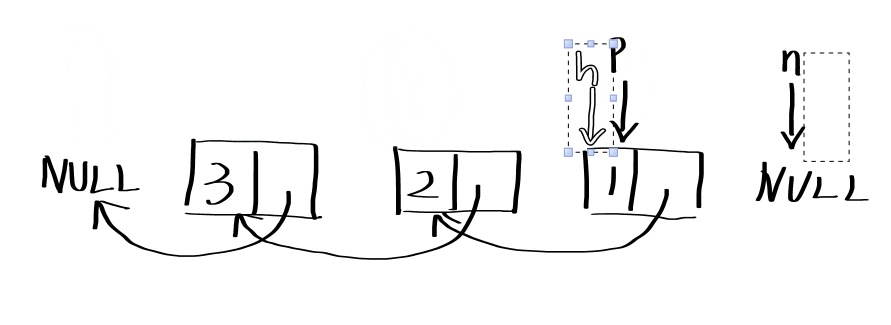
function ReverseList(pHead) {
    if (!pHead || !pHead.next) return pHead;
    let pre = null,
        next = null;
    while (pHead) {
        next = pHead.next;
        pHead.next = pre;
        pre = pHead;
        pHead = next;
    }
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12

# 2.2.2 递归解法

// 从尾部开始进行反转
function ReverseList(pHead) {
    if (!pHead || !pHead.next) return pHead;
    // 递归完后一直指向反转前的尾结点
    var pre = ReverseList(pHead.next);	
    // 反转
    pHead.next.next = pHead;
    // 避免死环
    pHead.next = null;
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11

递归过程：

pHead = 3, R(3)
			pHead = 2, R(2)
						pHead = 1, R(1)
						pre = 1
			2.next.next = 1(2->1)
            2.next = null(1X->X2)
3.next.next = 2(2->3)
3.next = null(3X->X2)

1
2
3
4
5
6
7
8

# 三、合并两个排序的列表

# 3.1题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

# 3.2 解法

function Merge(pHead1, pHead2) {
    if (!pHead1) return pHead2;
    if (!pHead2) return pHead1;
    if (pHead1.val <= pHead2.val) {
        pHead1.next = Merge(pHead1.next, pHead2);
        return pHead1;
    } else {
        pHead2.next = Merge(pHead1, pHead2.next);
        return pHead2;
    }
}